Función Inyectiva: Definición, Clases y Concepto Explicado

• Explorar la naturaleza de las funciones inyectivas abre una perspectiva fascinante en el universo de las matemáticas, enfocándose en aquellas funciones que garantizan la unicidad en la asignación de elementos entre conjuntos: cada elemento de un conjunto inicial se asocia de manera exclusiva con un elemento del conjunto final, sin repeticiones.
• Este concepto no solo fundamenta la teoría de conjuntos y la relación entre ellos, sino que también es crucial para comprender la diferencia esencial con sus contrapartes, las funciones no inyectivas, donde esta unicidad no se mantiene.
• Las clases de funciones matemáticas, incluyendo las inyectivas, sobreyectivas y biyectivas, se demarcan por características específicas que determinan su aplicación en diversos campos como la ciencia y la ingeniería, revelando su importancia al ofrecer métodos para análisis y solución de problemas mediante criterios de inyectividad y su contraposición.
• Además, se discuten técnicas para determinar la inyectividad, como el análisis algebraico y el uso de gráficas, proporcionando herramientas esenciales para profesionales y estudiantes.

Las funciones son la piedra angular de las matemáticas, actuando como puentes entre conjuntos y sus elementos. Una categoría particularmente fascinante de estas relaciones son las funciones inyectivas, que garantizan una correspondencia única y singular entre conjuntos. Este artículo desgrana su esencia, importancia y aplicación, llevando al lector a un viaje a través del universo de la lógica matemática.

De teoría de conjuntos a ingeniería, las funciones inyectivas juegan un rol crítico, modelando de forma precisa las relaciones uno-a-uno que son indispensables en campos tan diversos como la informática y la biología. ¿Pero qué hace a estas funciones únicas? Y más importante, ¿cómo se identifican y utilizan en escenarios reales? Acompáñanos a explorar estos interrogantes y más, mientras desvelamos el concepto de función inyectiva en su máxima expresión.

Definición de función inyectiva

Elementos de una función inyectiva

Una función inyectiva es definida formalmente como aquella relación entre dos conjuntos donde a elementos distintos del conjunto de partida se les asignan elementos distintos en el conjunto de llegada. Es decir, si (f(x) = f(y)) implica que (x = y), entonces la función (f) es inyectiva. Esta propiedad asegura una correspondencia uno-a-uno, excluyendo la posibilidad de que distintos elementos del dominio apunten al mismo elemento del codominio.

Los elementos clave en la operación de una función inyectiva son, por ende, el conjunto de partida o dominio, el conjunto de llegada o codominio, y la regla de correspondencia que define la asignación entre elementos de estos conjuntos. La esencia de la inyectividad yace en esta regla de correspondencia, distinguiéndose de otras funciones por su exclusividad en la asignación.

Importancia en las matemáticas

La inyectividad de una función no es simplemente una característica aislada; representa una herramienta fundamental en la construcción de teorías y en la solución de problemas dentro de las matemáticas y más allá. Las funciones inyectivas se utilizan para demostrar la unicidad de soluciones, para definir inversas de funciones, y como base en la teoría de números, algebra abstracta, y en la codificación de información.

Además, la capacidad de las funciones inyectivas para mapear elementos de manera única facilita la modelación de relaciones biunívocas, haciendo posible el estudio de la simetría, el orden y la estructura dentro de los sistemas matemáticos. Esta singular capacidad impulsa el avance tanto de la teoría pura como de sus aplicaciones prácticas.

Clases de funciones matemáticas

Comparación con funciones sobreyectivas

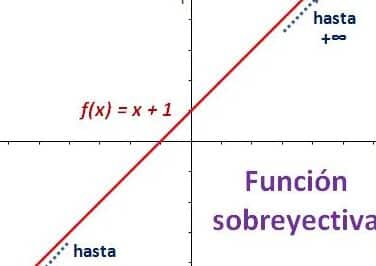
A diferencia de las funciones inyectivas, las funciones sobreyectivas o suryectivas, son aquellas donde cada elemento del codominio es imagen de al menos un elemento del dominio. En términos más coloquiales, en una función sobreyectiva todo el conjunto de llegada "está cubierto". La diferencia clave entre ambas radica en que, mientras la inyectividad enfatiza la unicidad en la asignación, la sobreyectividad se enfoca en la exhaustividad de la cobertura.

Esta distinción ilustra la versatilidad de las funciones matemáticas y la necesidad de categorizarlas según su comportamiento y propiedades. Cada tipo de función complementa y amplía nuestra comprensión de las relaciones entre conjuntos, proporcionando herramientas específicas para abordar una amplia gama de problemas y cuestiones.

Funciones biyectivas explicadas

Un escalón más allá, las funciones biyectivas combinan las propiedades de las inyectivas y las sobreyectivas. Una función es biyectiva si es a la vez inyectiva y sobreyectiva, estableciendo una relación uno-a-uno perfecta entre todos los elementos de los conjuntos implicados. Las funciones biyectivas no solo aseguran que cada elemento del dominio tiene un único correspondiente en el codominio, sino que también garantizan que cada elemento del codominio es alcanzado.

Desde una perspectiva matemática, las funciones biyectivas son el ideal, ya que facilitan la inversión de funciones y el estudio simétrico de las relaciones entre conjuntos. La biyectividad es un concepto poderoso, fundamental para el desarrollo de teorías matemáticas avanzadas y para aplicaciones en criptografía, teoría de la información y análisis combinatorio.

Características de las funciones inyectivas

Criterios de inyectividad

Una función (f: A rightarrow B) es inyectiva si, y solo si, dados dos elementos cualesquiera (x) y (y) de (A), la igualdad (f(x) = f(y)) implica que (x = y). Este criterio, conocido como la condición de inyectividad, es a la vez simple y profundamente significativo, ya que establece la base para la unicidad de la asignación en las funciones inyectivas.

La práctica de identificar la inyectividad de una función implica, por tanto, un examen cuidadoso de la regla de correspondencia para asegurarse de que cumple con la condición de inyectividad. Este examen es esencial para garantizar que la función en cuestión ofrece la singularidad deseada en las asignaciones.

Contraposición con funciones no inyectivas

En contraposición, las funciones no inyectivas permiten que dos o más elementos del dominio sean mapeados al mismo elemento del codominio. Este tipo de funciones, aunque útiles en ciertos contextos, carecen de la característica fundamental de la inyectividad: la garantía de una correspondencia uno-a-uno. La distinción entre funciones inyectivas y no inyectivas es, por tanto, una cuestión de unicidad versus duplicidad en las asignaciones.

Este contraste subraya la importancia de comprender las implicaciones y aplicaciones de la inyectividad, ya que determina la idoneidad de una función para modelar relaciones específicas entre conjuntos. La elección de una función inyectiva o no inyectiva dependerá del objetivo y de las características del problema en cuestión.

Ejemplos de aplicación de funciones inyectivas

Función inyectiva en teoría de conjuntos

En el ámbito de la teoría de conjuntos, las funciones inyectivas se utilizan para establecer relaciones de correspondencia uno-a-uno entre conjuntos de diferente naturaleza o tamaño. Un ejemplo clásico es la asignación de números identificativos únicos a elementos de un conjunto, garantizando que no haya duplicidades en la identificación.

Este tipo de aplicación no solo es crucial para el manejo eficiente de datos y la organización de colecciones, sino que también sienta las bases para el estudio matemático de la cardinalidad y del infinito. Las funciones inyectivas, así, facilitan la exploración de la estructura y las relaciones entre conjuntos de una manera ordenada y significativa.

Aplicaciones en ciencias e ingeniería

La utilidad de las funciones inyectivas trasciende la matemática pura, encontrando aplicaciones prácticas en campos como la ingeniería y las ciencias naturales. Por ejemplo, en la ingeniería de software, las funciones hash inyectivas son empleadas para asegurar la unicidad de las direcciones en la asignación de memoria, contribuyendo a la eficiencia y la seguridad de los sistemas informáticos.

En el campo de la biología, las funciones inyectivas permiten modelar relaciones exclusivas entre especies y sus características genéticas, facilitando el estudio de la herencia y la diversidad biológica. Estas aplicaciones muestran cómo la inyectividad puede ser una herramienta poderosa más allá de los confines teóricos, impactando positivamente en el desarrollo tecnológico y en la comprensión del mundo natural.

Métodos para determinar la inyectividad

Uso de gráficas en la evaluación

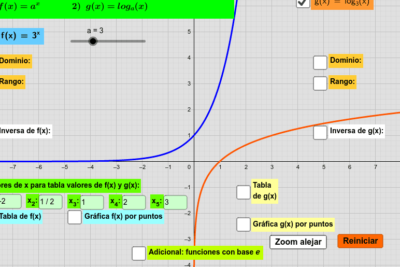
Una manera intuitiva y efectiva de determinar si una función es inyectiva consiste en el análisis de su gráfica. En términos generales, si una línea horizontal corta la gráfica de la función en más de un punto, entonces la función no es inyectiva. Este método gráfico, conocido como la prueba de la línea horizontal, proporciona un medio visual para evaluar la inyectividad de funciones, especialmente aquellas definidas en términos de variables reales.

La aplicación de esta técnica no solo facilita la comprensión de la inyectividad de una función, sino que también ilustra la conexión entre el concepto matemático y su representación gráfica. La prueba de la línea horizontal es, por tanto, un recurso valioso tanto para estudiantes como para profesionales al abordar problemas de inyectividad.

Análisis algebraico de la inyectividad

Además del enfoque gráfico, la inyectividad puede ser evaluada a través del análisis algebraico. Este método implica manipular la expresión matemática de la función para verificar si cumple con la condición de inyectividad (f(x) = f(y) Rightarrow x = y). El análisis algebraico requiere un entendimiento sólido de las propiedades de las funciones y de las operaciones algebraicas, pero ofrece un camino riguroso para determinar la inyectividad.

El uso del análisis algebraico es particularmente útil en contextos donde la función no puede ser fácilmente representada de manera gráfica o cuando se trabaja con conjuntos de alta dimensionalidad. Esta técnica proporciona un enfoque más abstracto pero profundo para examinar las propiedades de las funciones inyectivas.

Conclusión

Las funciones inyectivas son mucho más que una curiosidad matemática; son una herramienta esencial en la definición y análisis de relaciones entre conjuntos. Su capacidad para garantizar correspondencias uno-a-uno entre elementos las hace indispensables en una amplia gama de campos, desde la teoría de conjuntos hasta la ingeniería y las ciencias naturales. Al entender la definición, importancia y métodos para determinar la inyectividad, los estudiantes y profesionales pueden aplicar estos conceptos para resolver problemas complejos y discernir la estructura subyacente de los datos y fenómenos que estudian.

Las funciones inyectivas encarnan la belleza de la matemática: su capacidad para modelar el mundo de manera precisa y elegante. Al penetrar en el corazón de las relaciones matemáticas, revelan un universo de posibilidades que trasciende los límites de la imaginación, impulsando el avance del conocimiento humano hacia nuevos y emocionantes horizontes.

Video Relacionado sobre Funcion Inyectiva

FAQ Acerca de Funcion Inyectiva

1. ¿Cuándo es inyectiva una función?

Una función se considera inyectiva cuando asigna a cada elemento distinto del conjunto de partida un elemento único y diferente en el conjunto de llegada. Esto implica que en una función inyectiva no pueden existir dos elementos diferentes del conjunto de partida que tengan la misma imagen en el conjunto de llegada. La inyectividad es una característica crucial en diversas áreas de las matemáticas, ya que asegura una correspondencia uno a uno entre los elementos de dos conjuntos. Una forma práctica de identificar una función inyectiva es verificando que para cada valor de salida hay exactamente una entrada correspondiente. Esto significa que no hay valores repetidos de salida para entradas diferentes, lo que es fundamental en el análisis de funciones y en la resolución de ecuaciones donde la univocidad es necesaria.

2. ¿Qué ejemplos ilustran funciones inyectivas?

Para visualizar mejor la concepto de función inyectiva, consideremos el ejemplo de la relación entre personas y sus números de identificación. En este caso, a cada persona le corresponde un número de identificación único, lo que significa que no existen dos personas con el mismo número. Este es un ejemplo perfecto de una función inyectiva, donde cada elemento del conjunto inicial (personas) tiene asignado un elemento distinto y único en el conjunto final (números de identificación). Otro ejemplo sería la función matemática (f(x) = 2x + 3), donde cada valor de (x) produce un único resultado de (f(x)), sin que dos valores distintos de (x) compartan el mismo resultado de (f(x)). Estos ejemplos evidencian cómo la inyectividad se aplica tanto en situaciones cotidianas como en el estudio formal de funciones matemáticas.

3. ¿Cómo diferenciar entre funciones inyectivas y no inyectivas?

La principal diferencia entre funciones inyectivas y no inyectivas radica en la correspondencia de elementos entre los conjuntos de partida y llegada. En una función inyectiva, cada elemento del conjunto de partida se relaciona con un elemento único en el conjunto de llegada, asegurando una relación uno a uno. En contraste, una función no inyectiva permite que dos o más elementos del conjunto de partida compartan el mismo elemento en el conjunto de llegada, violando el principio de univocidad. Por ejemplo, la función (f(x) = x^2) no es inyectiva, ya que tanto (2) como (-2) producen el mismo resultado, (4). Identificar la naturaleza inyectiva de una función implica examinar su estructura y verificar visualmente o algebraicamente si cumple con el criterio de inyectividad.

4. ¿Qué importancia tienen las funciones inyectivas?

Las funciones inyectivas son fundamentales en varios campos de estudio debido a su propiedad de asignación única. Esta propiedad es especialmente relevante en álgebra y análisis matemático, donde la inyectividad facilita la inversión de funciones y garantiza la existencia de funciones inversas. En teoría de conjuntos, las funciones inyectivas permiten analizar y comprender la relación entre los tamaños de conjuntos distintos. Además, en informática, las funciones inyectivas se utilizan para generar códigos y claves únicas en la programación y el cifrado de datos, garantizando la seguridad de la información transmitida. En estos contextos, la inyectividad asegura correspondencias claras y definidas, lo que es crucial para el análisis, la interpretación y la aplicación práctica de conceptos matemáticos.

5. ¿En qué se diferencia una función inyectiva de una biyectiva?

Si bien ambas funciones, inyectivas y biyectivas, comparten la característica de tener correspondencias únicas, difieren en dos aspectos fundamentales: el primero es que mientras en la función inyectiva cada elemento del conjunto de partida se relaciona con un elemento único en el conjunto de llegada (sin requerir que todos los elementos del conjunto de llegada tengan una preimagen), una función biyectiva asegura adicionalmente que cada elemento del conjunto de llegada está relacionado con exactamente un elemento del conjunto de partida, cubriendo así todo el conjunto de llegada. En otras palabras, una función biyectiva es tanto inyectiva como sobreyectiva, garantizando una correspondencia uno a uno perfecta entre los conjuntos, lo que significa que es una función inyectiva que también es sobreyectiva. Esta distinción es crucial en el estudio de las funciones y sus aplicaciones, ya que determina la posibilidad de invertir funciones y establecer correspondencias totales entre conjuntos.

Si quieres conocer otros artículos parecidos a Función Inyectiva: Definición, Clases y Concepto Explicado puedes visitar la categoría MATEMÁTICAS.